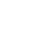要注意了,工程測量的坐標系和數學坐標系在定義上是有區別的,因此在計算公式上也有區別。定義的區別如下圖:
為啥這樣定義?很難找到結果,就當約定俗成吧。除非你某一天能把它約定回來,不然咱還是遵守吧。
這個定義很坑,如果直接繪制在CAD里,左右會和實際相反,我們在將測量坐標繪入CAD時,只好將xy交換后繪圖,這樣繪制的圖形才和實際相吻合。
你除了知道坐標(x,y)之外,還有一個重要的東東要知道,不知道這個東東,你的工程測量只能算門外漢。嗯,那就是坐標方位角。
無圖無真相啊,咱先看一張圖。
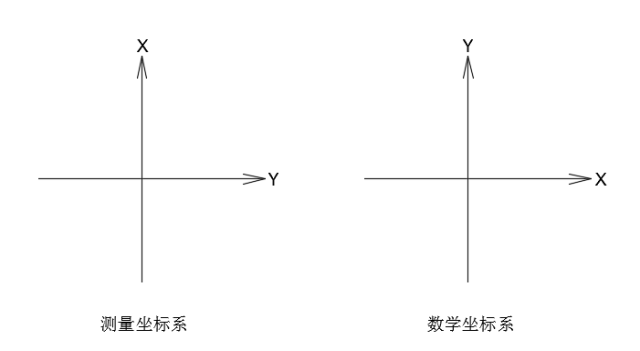
坐標方位角僅指一個方向,其值等于將坐標系原點平移至該方向起點,坐標零方向順時針旋轉到該方向的角度。
是不是還是難以理解?腦子里放一個線段,把測量坐標系的圖移過去,原點與一個端點重合,從x方向開始想象有一條線順時針旋轉到與線段重合,旋轉的角度就是與原點重合的點到另一點的方位角的值。
方位角的取值范圍:0-360度,一般沒有360度的方位角,因為到360度時又記為0度。
還有一個簡便計算的特征:A到B的方位角=B到A的方位角+180度。這個特征在坐標推算時會用到的。
在工程測量坐標系里,一般你需要掌握以下三種計算:
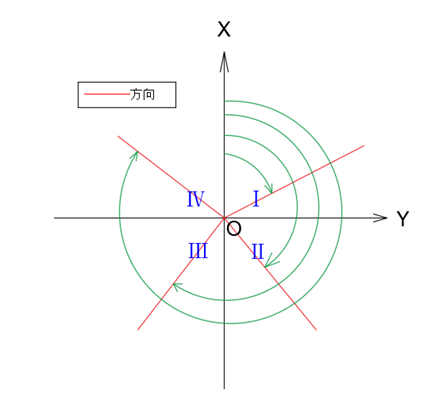
坐標正算是指已知起算點的坐標及至目標點的距離和方位角,計算目標點的坐標。看一下圖更容易理解。

公式很簡單:
X=x+s*cosF
Y=y+s*sinF
XY:待求點的xy;
x:已知點的xy;
s,F:已知點到待求點的距離和方位角。
坐標反算可以看作是坐標正算的逆運算,指已知起算點和目標點的坐標,計算起算點到目標點的距離和方位角。再看一張圖:
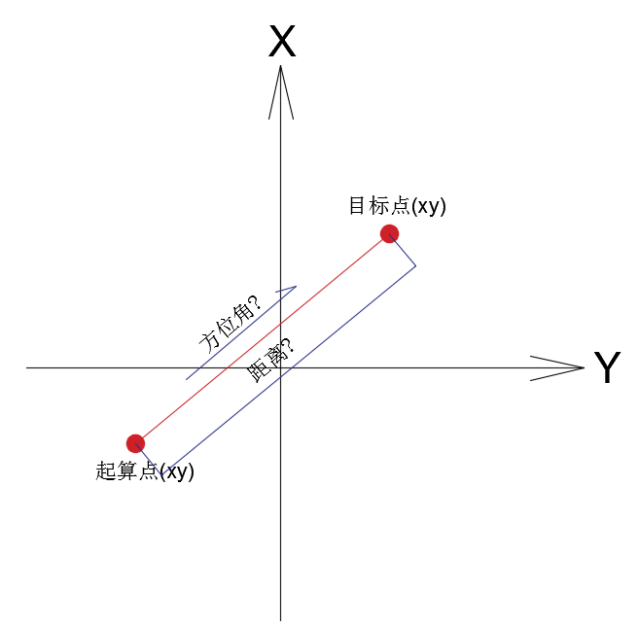
距離的計算相對簡單:s=sqrt((x1-x2)^2+(y1-y2)^2))
sqrt:開算術平方根;
^:乘方的運算符號。
方位角的計算要稍復雜一點,其實也很簡單。
先計算一個角度值:F=atan((y2-y1)/(x2-x1)),如果F為負,加360度即可。然后判斷一下x2是否比X1小,如果小,F則加180度,否則不變。
atan:反正切。
鄙視一下:如果x2=x1,上面的公式還能用嗎?這時F=90度,判斷跟上面相同。
這個點比較難,要用到高中的數學知識。如果你具備高中及以上學歷,就繼續看下去吧。
坐標變換是指將一個坐標系里的坐標變換到另一個坐標系里,這在工程測量中常常用到,且可能帶來想不到便宜效果。
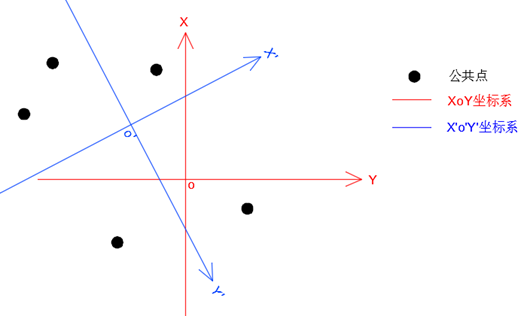
先看一個數學公式:
x2=x1cosα+y1sinα+A
y2=y1cosα-x1sinα+B
x1,y1:第一個坐標系的xy;
x2,y2:第二個坐標系的xy;
α:坐標系的旋轉角;
A,B:坐標原點的平移值。
這就是初等數學里坐標系的旋轉和平移公式,放到工程測量里面來,多了一些測量的概念,當然如果簡單應用,跟初等數學并沒有區別。
在實際的工作中,并沒有現成的旋轉角和平移值供我們使用,因此利用公式直接計算會很困難。腫么辦呢?我們只有利用公共點計算旋轉角和平移值,從而解算其他未知點。所謂公共點,是指該點同時具有兩個坐標系的坐標,在實際中很容易根據定義或計算獲得。
現在我們已知兩個公共點進行轉換公式推導:
假定A坐標系兩點坐標為(x1,y1)(x2,y2),與之對應的B坐標系坐標為(x11,y11)(x21,y21)
令 a = x21 - x11 : b = y21 - y11 : c = x2 - x1 : d = y2 - y1
如果 c ^ 2 + d ^ 2=0,則轉換無效。否則進行轉換計算:
令 u = (a * c + b * d) / (c ^ 2 + d ^ 2) v = (a * d - b * c) / (c ^ 2 + d ^ 2) w = x11 - x1 * u - y1 * v : z = y11 + x1 * v - y1 * u
已知A坐標系一點坐標(yizhix,yizhiy),計算該點在B坐標的坐標(x,y)
x = yizhix * u + yizhiy * v + w
y = (-1) * yizhix * v + yizhiy * u + z
真的很簡單,這在日常工地上已經足夠使用了!
來源:工程測量之家(侵刪)